Decoding the Digital Realm: Hexadecimal Conversion Explained

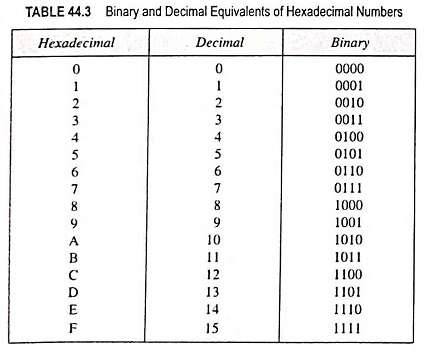
Source: eeeguide.com

Ever felt like you're speaking a secret language when you see those funky hexadecimal numbers? You're not alone! Understanding hexadecimal (often just called hex) is like unlocking a hidden door to the world of computer programming and digital design. This guide breaks it down, making it easy for you to translate.

What is Hexadecimal?

Hexadecimal is a base–16 number system. (Imagine it like counting using only sixteen different digits instead of ten.) It's awesome for computers because it lets them represent a big chunk of data in a short, simple code. Think of it as a digital shorthand.

Source: amazonaws.com

Why use Hexadecimal?

1. It's concise. It represents more data with fewer symbols.
2. Computers "like" it. Computers love converting back and forth.
3. Web designers use it to display colours in the HTML language.
4. Handy for programmers, for describing memory addresses.

Decimal, Binary, and the Hex Connection

Understanding the link between decimal (the base-10 system we use), binary (base-2), and hex is important to understand hexadecimal conversion.

From Decimal to Binary and Back (the foundation!)

First, we'll learn how to convert decimal numbers to binary. This will help later in the hex process.

1. Dividing method: Divide the decimal number by 2, recording the remainder. Repeat until the quotient is zero.

Example: Converting 13 (decimal) to binary

• 13 / 2 = 6 remainder 1
• 6 / 2 = 3 remainder 0
• 3 / 2 = 1 remainder 1
• 1 / 2 = 0 remainder 1

Reading the remainders from bottom to top gives you the binary equivalent of 13: 1101

(To do this conversion backwards – converting binary back to decimal, look at how big the 2 power is.)
Now we have binary, we move to our goal – Hex conversion.

Hexadecimal Digits: The 0-9 A-F Alphabet!

1. 0-9: Like our normal digits
2. A=10
3. B=11
4. C=12
5. D=13
6. E=14
7. F=15

(Remember, hex is base-16, so our alphabet goes all the way up to 15!).

Conversion to and from Hex

Now that we understand our building blocks, we can build. Let's talk about hexadecimal conversion steps!

Converting from Decimal to Hexadecimal (the step-by-step guide)

Let's use 255 as an example:

1. Divide by 16:
   255 / 16 = 15 remainder 15

2. Now, look at the remainders in hexadecimal (the new ones for hexadecimal only! don't forget to take look at the table again!) . 15 = F.

3. Write your result: The result is F1 (always read from bottom to top)

Source: princeton.edu

(This makes sense since 255=15×16^1 + 15)

Converting from Hexadecimal to Decimal (unpacking the hexadecimal)

Want to go from hexadecimal back to normal? (Decimal number)

Let's pick A5. (remember that A equals 10 and 5 equals 5!).

1. Establish the decimal values A equals 10 and 5 remains 5 in hexadecimal (which gives decimal conversion in that matter too, you've learned so far)

2. Apply powers of 16: In this scenario it should be: A = (10 * 16¹) + (5*16⁰)

3. Calculating the decimal value Doing that calculation should yield (160 + 5), which equals 165

   

   Source: vlsifacts.com

Why do we need this, seriously?

The importance of knowing hex in computing and related areas:

• Memory addresses (you know, computer locations in memory?) computers show memory in hexadecimal values!
• Color codes: For representing colours in website development, hex numbers show colors on screens, as code numbers. (Website colours)
• Data representation: For describing data and for programmers.
• Binary file contents (this may not always have so many hex code!)

Conversion Example – More Complex Conversion

Converting 10230000 to hexadecimal.

(Let's go in steps: Divide by 16 then take look at the reminders as hexadecimal in decimal conversion.)

• Divide 10,230,000 by 16, with remainders (again, using repeated division).
• Writing the result will result in a massive string of numbers!

(You see how cool hex is? Like using a superpower of short coding!)

Practice Makes Perfect: Try These!

Test your newfound hex skills!

• Convert 357 (decimal) to hexadecimal.
• Convert C8 (hexadecimal) to decimal.
• Now that you know both conversion directions (which may include more than these), try your own to show how confident you are now!)

Troubleshooting: Common Hex Conversion Mistakes

1. Forgetting to put numbers to the correct power of 16.
2. Incorrect interpretation of hexadecimal alphabet (e.g., F=15, not 6 or 7).

Conclusion

Congratulations! You've taken a deep dive into the world of hexadecimal conversion! Now, you can speak the language of computers and even designers, too! Remember that practicing regularly is crucial! Like any skill, conversion from decimal to hex (and vise versa!) improves with repetition, like cycling to help strengthen your muscles or to take to a different level or proficiency! It is so much easier and less intimidating, I must say that, to know and understand the concepts, to move from beginner level into intermediate level proficiency to become an expert in it! This was a simple step-by-step introduction to Hexadecimal (Hex) and hopefully it should inspire your interest to find out even more and you continue your journey learning more!