Converting Hexadecimal to Binary: A Simple Guide

Ever felt lost in the digital world of computers, with all those weird symbols like "A," "F," and "10"? Don't worry! Converting hexadecimal to binary is a manageable task. It's like learning a secret code – once you understand it, it's really easy.

Understanding the Two Systems

Hexadecimal and binary are both number systems, but they use different bases (that's a fancy word for how many symbols are in the system):

• Binary uses base 2, meaning it only has two symbols: 0 and 1.
• Hexadecimal uses base 16, having 16 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F.

(Think of decimal – we all know that one!)

Why Hexadecimal?

Using hexadecimal, you can shorten a long sequence of binary code – like writing the full sentence "A big house," instead of saying "A B I G H O U S E." (it is more organized this way!) So imagine how easy this could be for computers.

Why Binary?

Binary is the language that computers truly understand. (They only understand zeroes and ones – their basic elements.) This way of using zeroes and ones is essential for all of the actions of the machine. It's a very fundamental process.

Steps to Convert Hex to Binary

Source: wikihow.com

Here's how to change hexadecimal to binary (remember those hexadecimal digits?):

Step 1: Understanding Hexadecimal Digits

Firstly, you need to know the hexadecimal value of the number (remember that in the hexadecimal number system, numbers greater than 9 are replaced by alphabetic letters (A = 10, B = 11…)).

Step 2: Converting Each Hex Digit to Four Binary Bits

Source: wordpress.com

The real magic here is knowing that each hexadecimal digit represents four bits (binary digits).

<table>

Hexadecimal Binary 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 A 1010 B 1011 C 1100 D 1101 E 1110 F 1111

Step 3: Convert each Hex Digit into Its Binary Equivalent.

Let's say you have the hexadecimal number "3F7".

Step 3: Here, we convert the first hexadecimal digit '3' from the example ("3F7") into its 4-bit equivalent: '3' = "0011".

Step 4: Next, do it for the 'F' from the example. (Remember the chart!): 'F' = "1111".

Step 5: Repeat it for the final number ('7'): '7' = "0111".

Step 4: Combining the Binary Results

Finally, you simply place these together: "3F7" becomes "001111110111".

This "001111110111" is the binary equivalent of the original hexadecimal number! You have succeeded.

Example: Convert 2AF to Binary

1. Identify the Hex Digits: We have 2, A, and F.

2. Convert each Hex Digit to its Binary Form

• 2 is 0010
• A is 1010
• F is 1111

3. Combine the results: 0010 1010 1111

4. Result: 2AF in binary is 001010101111

More Complex Examples:

Source: slidesharecdn.com

Let's try converting "1A3F".

1. Separate Digits: 1, A, 3, F

2. Convert to Binary:

   • 1 = 0001
   • A = 1010
   • 3 = 0011
   • F = 1111

3. Combine the binary representation: 0001 1010 0011 1111

4. Result: "1A3F" in binary equals "0001101000111111"

Source: cloudfront.net

Practice Makes Perfect

Now try converting other hexadecimal numbers on your own – like these:

1. Example #1: Convert "4D".
2. Example #2: Convert "72A".

(Note the result and use your learning to get it! I hope you get it!)

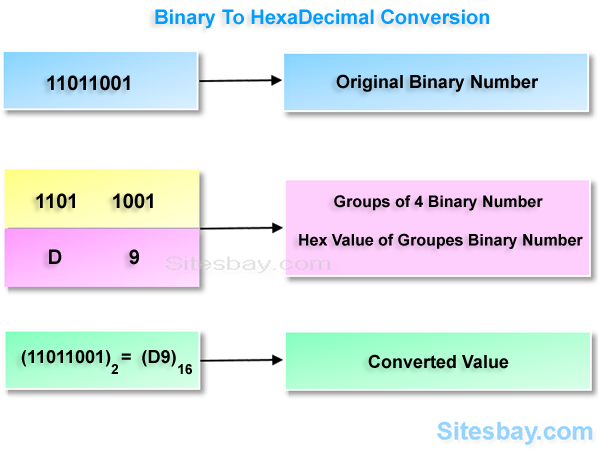
Source: sitesbay.com

Key Takeaway

(I like that converting hexadecimal to binary is so direct – it's actually a bit more straightforward!)

Converting hexadecimal to binary is a pretty important concept – like learning any new code, the first attempt might take longer than following, but you will find you'll get the hang of it in time with repeated practice and memorization (just like a code!). Knowing how to convert these different number systems can really broaden your digital comprehension – (that means getting more familiar and comfortable with digital coding!)

This guide has shown you step by step, and through practice you'll become better! And finally you have all the tools to do the tasks required on your own! I am here to support you with additional tasks or inquiries you have in your quest! I encourage you to give these examples a try. If you have any other examples, you can try and ask questions too! Good luck with the conversion tasks!