convert hex to number

Converting Hexadecimal to Numbers: A Beginner's Guide

Ever wondered how computers store colors or other data? You're about to discover! (It's super interesting!) We'll be translating those mysterious hex codes into everyday numbers. It's like unlocking a secret code.

Table of Contents

Understanding Hexadecimal

Hexadecimal (or "hex") is a number system using 16 digits. (Unlike our regular decimal system, which uses 10 digits from 0 to 9.) Hex uses 0-9 and then A, B, C, D, E, F.

What is a number system?

A number system is a way to represent numbers using symbols. Each system has a set of symbols (like digits).

Decimal uses 0 to 9.
Binary uses 0 and 1.
Hexadecimal uses 0-9 and A-F.

Why use hex?

Source: ytimg.com

Computers "think" in binary (only 0s and 1s). Hex is handy for humans (we understand decimal), making complex binary data easier to read and write.

The Conversion Process: From Hex to Decimal

Turning hex to decimal is all about understanding each digit's "place value".

Steps for Conversion

Identify each hex digit: Look at your hex number. Let's say it's "A3F."
Determine the power of 16: Each position in a hex number corresponds to a power of 16. The rightmost digit is 16⁰ (or just 1), the next is 16¹, the next is 16².
- For example: in "A3F," the F digit has a place value of 16⁰. The 3 is 16¹, and the A has a place value of 16².
Convert hex digits to decimal equivalent: Replace each letter (A-F) with its decimal value. A is 10, B is 11, C is 12, D is 13, E is 14, and F is 15.
Multiply: Now, multiply each hex digit by its corresponding power of 16 and add them up!
```
Example:

A3F  =  (10 * 16²) + (3 * 16¹) + (15 * 16⁰) 
    =   (10 * 256) + (3 * 16) + (15 * 1)
    =    2560 + 48 + 15
    =  2623
```
That's how the hex value "A3F" translates into the decimal number "2623".

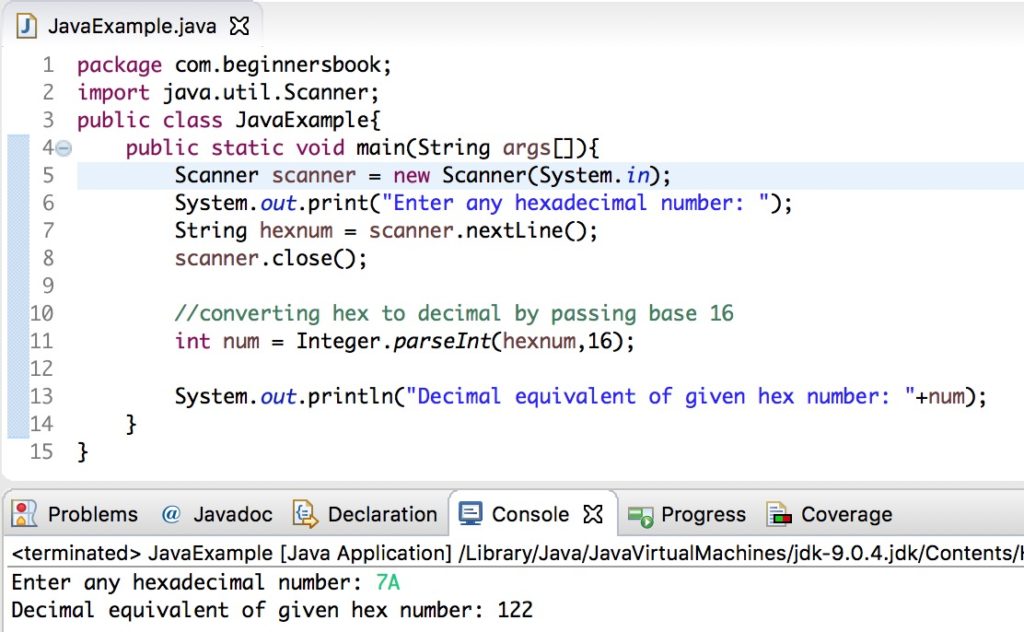
Source: beginnersbook.com

Converting other hex values: Example Cases

Let's explore a few more cases, just to get the idea! (Practice makes perfect!)

Example 1: 1A

First digit is 1.
Second digit is A (or 10 in decimal).

Using our formula:

(1 * 16^1) + (10 * 16^0)
=  1 * 16 + 10 * 1
=   16 + 10 = 26.

Decimal value = 26.

Example 2: FF

First digit is F (or 15 in decimal).
Second digit is F (or 15 in decimal).

Calculations:

 (15 * 16^1) + (15 * 16^0)
 = 15 * 16 + 15 * 1
 =   240 + 15 = 255

Decimal value = 255.

Common Mistakes and Troubleshooting

Source: cloudfront.net

Mixing up powers of 16: Be careful with exponents. Each place value in hex corresponds to a different power of 16.
Remembering hex equivalents: Remember the letter to number mappings!

When would you need to do hex to decimal conversion?

Source: wikihow.com

You'll frequently encounter hex in situations dealing with computers or web development (for example, for color codes on web pages). Understanding how these code work helps you "read" these data representations, (instead of just typing randomly) making it easier to change them, solve problems with color displays etc. Hex and decimal are not completely separate worlds though (they often work together and overlap)!

Applying what we have learned – Case Study: Website Colors

Web developers use hex codes for colors on web pages.

Let's say the color is expressed as "#FF9900"

This is not the normal number. It's a bit trickier to get used to when there are "extra parts"(that have different roles than the parts we practiced so far.). This # represents the start. FF9900 in reality can be broken down and converted into parts as below :

FF represents the intensity of Red
99 represents the intensity of Green
00 represents the intensity of Blue

We only looked into conversion for whole hexadecimal values, to keep this beginner friendly! (And remember these bits could be processed by machines that don't really even need our conversion in many situations – they are already programmed to 'know').

Now, let's say, instead, that the whole color code were A50 , we can follow the exact same procedure like this

Isolate the individual values.
Substitute each hex character with its corresponding decimal value.
Perform the necessary calculations to arrive at the result.

Java Basic Image Exercise

Source: w3resource.com

Remember the "place value" concepts discussed earlier to arrive at the correct decimal values. (There is one more important point: we're dealing with a particular "base-16" system – for which we might use a different number structure).

Final Thoughts

You can do it! Understanding hex to decimal conversion is essential for handling digital data more efficiently, just remember the place values! Conversion isn't just about numbers – understanding different number systems connects different aspects of the world of computation – with us doing the calculations as "middlemen" to help the computer and its users! If you got stuck at any part of this, always seek more help and do extra practices; you can go really far (if you just don't stop and never quit)! Keep practicing these examples to improve and never quit – you will soon see how these processes and topics could open up exciting new things for you.

converthex.online