Converting Hexadecimal to Floating-Point Numbers

Ever wondered how those cryptic hexadecimal codes translate into the numbers we use every day? Like, you know, the ones with decimals and stuff? Well, you're in the right place. This guide dives deep into converting hexadecimal values into floating-point representations, breaking it down into easy steps!

Understanding the Basics

What's Hexadecimal?

Source: howtodoinjava.com

Hexadecimal, or "hex," is a number system using base–16. It uses 16 symbols to represent values – 0-9 and A-F (representing 10–15 in decimal). (It's way shorter than using base-10 for complex numbers).

What's Floating-Point?

Floating-point numbers, also called floats, represent numbers with a decimal point, allowing for both very small and very large numbers (like the mass of an electron or the distance to the moon). They are how many computer programs store many real numbers.

Why Convert?

Different programs, applications, or systems use different data types to represent and interpret data. Sometimes you need to move numbers from one format (like hex) to a format that works best for calculations or storage.

Hex to Decimal: The Bridge

Source: wordpress.com

Before floating-point conversion, we need to change our hex code to the friendly decimal representation. (Decimals make it so much easier).

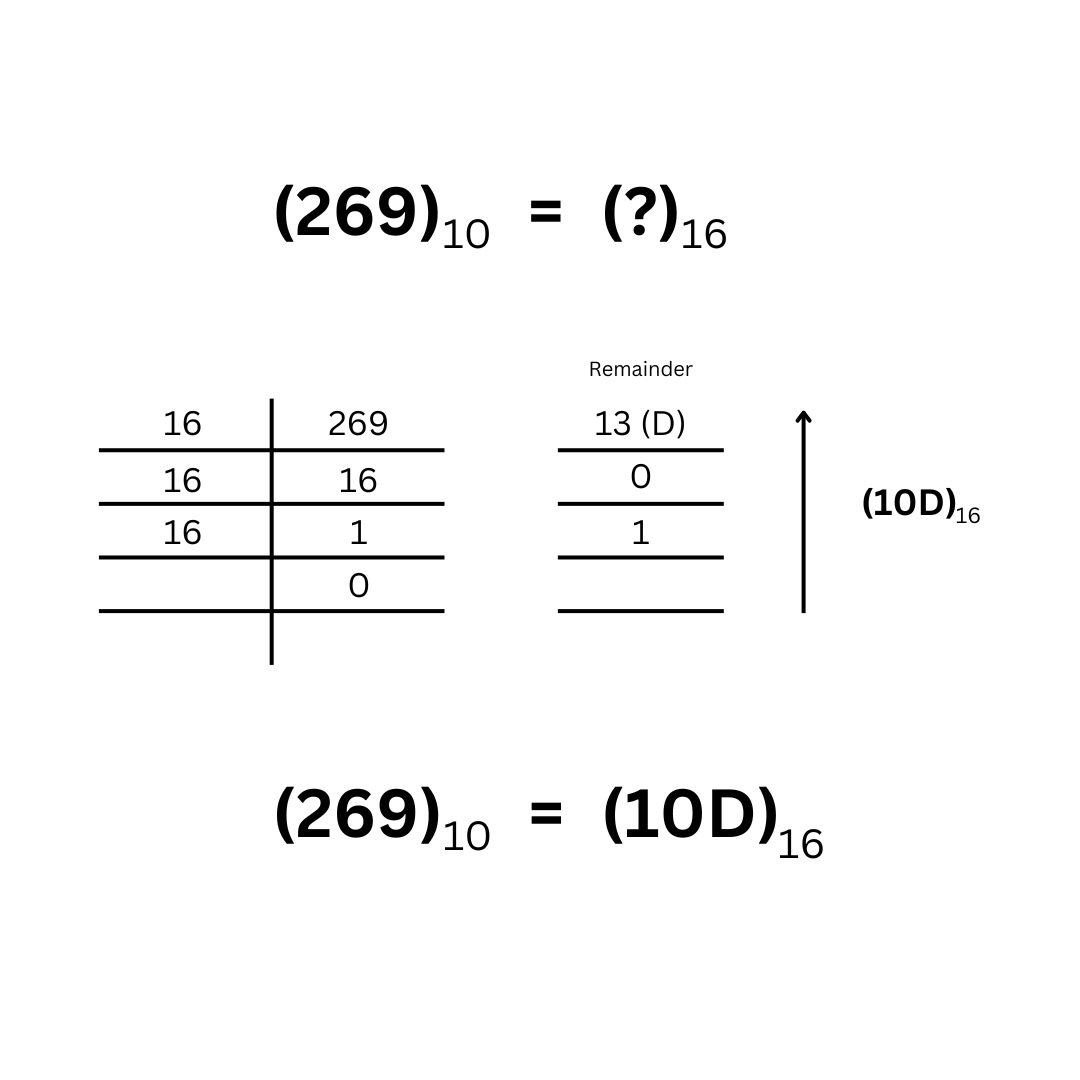
Steps to Decimal Conversion

Source: codescracker.com

1. Write down your hex value. (Like, A1F3)

2. Assign powers of 16 to each digit. From right to left, start with 16^0 and keep incrementing the exponent.

   • A (represents 10 decimal) = 10 × 16^3
   • 1 = 1 × 16^2
   • F (represents 15 decimal) = 15 × 16^1
   • 3 = 3 × 16^0

3. Do the multiplication. Calculate the value for each digit in your hex, by multiplying that digit by the associated power of 16 and add them.

Decimal = (10 x 16^3) + (1 x 16^2) + (15 x 16^1) + (3 x 16^0)
Decimal = 40960 + 256 + 240 + 3
Decimal = 41260 (wow, big!)

Decimal to Floating-Point: A Bit More Complicated

Source: postimg.cc

This step is the meat and potatoes (no pun intended!). Remember: you have a decimal now.

The Parts of a Floating-Point Number

Floating-point numbers (using IEEE-754 standards!) have these key components:

• Sign Bit: 1 bit (0 for positive, 1 for negative)
• Exponent: Several bits, determining magnitude.
• Mantissa: Several bits, providing the fractional part.

Understanding IEEE 754

Source: ytimg.com

The IEEE 754 standard precisely dictates how floating-point numbers are represented in computers (this prevents confusion or data corruption between systems, kinda like using a common language). This standardization guarantees consistent floating-point calculations across platforms. (Makes a programmer's life much easier!)

Converting in Detail (Hex to Float)

Let's say our hex code is (still remembering to use '1A12) for decimal now..

1. Decimal conversion: As per steps above (1a12hex is 6746)

2. Understanding the format (IEEE-754 32-bit):
   Look for the representation according to IEEE-754.

3. Splitting the decimal number: Convert 6746 into binary.

4. Normalizing the number:
   Write your binary value like "1.xxxxx" (mantissa part)

5. Calculating exponent: Adjust (by adding/subtracting the bias from the actual exponent) the binary representation. The standard has a 'bias' you have to add, and we want to determine where the 'dot' will be positioned in the decimal form and to add or minus that to the number of the position after the first '1'.

   • If decimal part >= 0: position the dot in that position
     and the result should look like (+).mmmmmmmm

   • If decimal part < 0, remove those sign. position the dot after first significant bit (no leading 0),
     and the result should look like (-).mmmmmmmm

(Example with binary (I recommend to get accustomed to these): Converting '0x1234' (decimal: 4660).

(To make sure your floating point conversion is working, try different examples or utilize calculators designed for hex to floating-point conversions (some websites might help out!).)

Why would these steps differ or matter in different programming languages?
(Programming languages are made by different people with their own perspectives).
There can be little details that are adjusted (if needed), for different formats.

Tools for Conversion

Tools make our work easier, it does a lot more math! A web-based converter, or tools found in programming environments or in dedicated floating-point calculator can also work as well for conversions from one format (decimal) to other formats like floating point). Just plug your hex value in to these programs for easier results, sometimes you want your answers in a specific format, like decimal-float/scientific/normalized binary etc (they could sometimes handle).

Conclusion: Putting it all Together

Remember these steps for Converting hex to float-point

1. Converting hex to decimal
2. Determining binary representation,
3. Placing exponent according to the standard rules
4. Calculate (to obtain) the significand part

It takes several steps to transform a simple hex code into a complete float, however the entire point (is that if one thing makes life more complicated, then just let there be simpler tools.)

Converting hexadecimal numbers to floating-point can seem challenging at first. Just remember all the simple rules. And take things step by step! With practice, you'll be an expert in converting between these systems in no time! Good luck.